PENGERTIAN DAN SEJARAH
KALKULUS
Kalkulus (Bahasa
Latin: calculus, artinya "batu kecil", untuk menghitung)
adalah cabang ilmu matematika yang mencakup limit, turunan, integral,
dan deret tak terhingga. Kalkulus adalah ilmu mengenai perubahan, sebagaimana
geometri adalah ilmu mengenai bentuk dan aljabar adalah ilmu mengenai
pengerjaan untuk memecahkan persamaan serta aplikasinya. Kalkulus memiliki aplikasi yang
luas dalam bidang-bidang sains, ekonomi, dan teknik; serta dapat memecahkan
berbagai masalah yang tidak dapat dipecahkan dengan aljabar elementer.
Kalkulus
memiliki dua cabang utama, kalkulus diferensial dan kalkulus integral yang
saling berhubungan melalui teorema dasar kalkulus. Pelajaran kalkulus adalah
pintu gerbang menuju pelajaran matematika lainnya yang lebih tinggi, yang
khusus mempelajari fungsi dan limit, yang secara umum dinamakan analisis
matematika.
Sejarah
perkembangan kalkulus bisa ditilik pada beberapa periode zaman, yaitu zaman
kuno, zaman pertengahan, dan zaman modern. Pada periode zaman kuno, beberapa
pemikiran tentang kalkulus integral telah muncul, tetapi tidak dikembangkan
dengan baik dan sistematis. Perhitungan volume dan luas yang merupakan fungsi
utama dari kalkulus integral bisa ditelusuri kembali pada Papirus Moskwa Mesir
( 1800 SM ) di mana orang mesir menghitung volume piramida terpancung,
Archimides mengembangkan pemikiran ini lebih jauh dan menciptakan heuristik
yang menyerupai kalkulus integral.
Pada zaman
pertengahan, matematikawan India, Aryabhata, menggunakan konsep kecil tak
terhingga pada tahun 499 dan mengekspresikan masalah astronomi dalam bentuk
persamaan diferensial dasar. Persamaan ini kemudian mengantar Bhĕskara II pada
abad ke-12 untuk mengembangkan bentuk awal turunan yang mewakili perubahan yang
sangat kecil takterhingga dan menjelaskan bentuk awal dari "Teorema Rolle".
Sekitar tahun 1000, matematikawan Irak Ibn al-Haytham (Alhazen) menjadi orang
pertama yang menurunkan rumus perhitungan hasil jumlah pangkat empat, dan
dengan menggunakan induksi matematika, dia mengembangkan suatu metode untuk
menurunkan rumus umum dari hasil pangkat integral yang sangat penting terhadap
perkembangan kalkulus integral. Pada abad ke-12, seorang Persia Sharaf al-Din
al-Tusi menemukan turunan dari fungsi kubik, sebuah hasil yang penting dalam
kalkulus diferensial.
PRINSIP DASAR KALKULUS
Definisi limit:
kita katakan bahwa limit f(x) ketika x mendekati titik p adalah L apabila untuk
setiap bilangan & epsilon; > 0 apapun, terdapat bilangan & delta;
> 0, sedemikian rupanya: Kalkulus pada umumnya dikembangkan dengan memanipulasi
sejumlah kuantitas yang sangat kecil. Objek ini, yang dapat diperlakukan
sebagai angka, adalah sangat kecil. Sebuah bilangan dx yang kecilnya
tak terhingga dapat lebih besar daripada 0, namun lebih kecil daripada bilangan
apapun pada deret dan bilangan real positif apapun. Setiap perkalian dengan
kecil takterhingga (infinitesimal) tetaplah kecil tak terhingga, dengan kata
lain kecil tak terhingga tidak memenuhi properti Archimedes.
Dari sudut
pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi kecil tak
terhingga. Pada abad ke-19, konsep kecil tak terhingga ini ditinggalkan karena
tidak cukup cermat, sebaliknya ia digantikan oleh konsep limit. Limit
menjelaskan nilai suatu fungsi pada nilai input tertentu dengan hasil dari
nilai input terdekat. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik
memanipulasi limit-limit tertentu. Secara cermat, definisi limit suatu fungsi
adalah: Diberikan fungsi f(x) yang terdefinisikan pada interval di
sekitar p, terkecuali mungkin pada p itu sendiri. Kita mengatakan bahwa
limit f(x) ketika x mendekati p adalah L, dan menuliskan:jika, untuk
setiap bilangan & epsilon; > 0, terdapat bilangan δ > 0
yang berkoresponden dengannya sedemikian rupanya untuk setiap x.
BENTUK-BENTUK KALKULUS
Kalkulus
merupakan sebuah cabang ilmu dari matematika yang sangat dibutuhkan untuk
pengembangan ilmu pengetahuan terutama bagi fisika danektik (Engineering).
Dalam ilmu kalkulus yang dapat kita pelajari antara lain :
Garis singgung pada (x, f(x)). Turunan f'(x) dari sebuah
kurva pada sebuah titik adalah kemiringan dari garis singgung yang menyinggung
kurva pada titik tersebut.
1.
Kalkulus
Diferensial
Kalkulus
diferensial adalah ilmu yang mempelajari definisi, properti, dan aplikasi
dari turunan atau kemiringan dari sebuah grafik. Konsep turunan secara fundamental lebih
maju dan rumit daripada konsep yang ditemukan di aljabar. Dalam aljabar,
seorang murid mempelajari sebuah fungsi dengan input sebuat angka dan output
sebuah angka. Tetapi input dari turunan adalah sebuah fungsi dan outputnya juga
adalah sebuah fungsi.
Untuk memahami
turunan, seorang murid harus mempelajari notasi matematika. Dalam notasi
matematika, salah satu simbol yang umumnya dipakai untuk menyatakan turunan
dari sebuah fungsi adalah apostrofi. Maka turunan dari fadalah f'.
Jika input dari
sebuah fungsi adalah waktu, maka turunan dari fungsi itu adalah laju perubahan
di mana fungsi tersebut berubah. Jika fungsi tersebut adalah fungsi linear, maka fungsi
tersebut dapat ditulis dengan y=mx+b, di mana:
ini memberikan nilai dari kemiringan suatu garis lurus. Jika sebuah fungsi bukanlah garis lurus, maka perubahan y dibagi terhadap perubahan x bervariasi, dan kita dapat menggunakan kalkulus untuk menentukan nilai pada titik tertentu. Kemiringan dari suatu fungsi dapat diekspresikan:
ini memberikan nilai dari kemiringan suatu garis lurus. Jika sebuah fungsi bukanlah garis lurus, maka perubahan y dibagi terhadap perubahan x bervariasi, dan kita dapat menggunakan kalkulus untuk menentukan nilai pada titik tertentu. Kemiringan dari suatu fungsi dapat diekspresikan:
di mana koordinat dari titik pertama adalah (x, f(x)) dan h adalah jarak horizontal antara dua titik. Untuk menentukan kemiringan dari sebuat kurva, kita menggunakanlimit:
2. Kalkulus integral
Kalkulus
Integral adalah ilmu yang mempelajari definisi, properti, dan aplikasi dari dua
konsep yang saling berhubungan, integral taktentu dan integral
tertentu. Proses pencarian nilai dari sebuah integral
dinamakan pengintegralan (integration). Dengan kata lain, kalkulus
integral mempelajari dua operator linear yang
saling berhubungan. Integral taktentu adalah antiturunan, yakni kebalikan dari
turunan. F adalah integral taktentu dari f ketika f adalah
turunan dari F. Integral tertentu memasukkan sebuah fungsi dengan outputnya
adalah sebuah angka, yang mana memberikan luas antar grafik yang dimasukkan
dengan sumbu x. Contohnya adalah jarak yang ditempuh dengan lama waktu tertentu
|
Jika
kecepatannya adalah konstan, perhitungan bisa dilakukan dengan perkalian, namun
jika kecepatan berubah, maka diperlukan sebuah metode yang lebih canggih. Salah
satu metode tersebut adalah memperkirakan jarak tempuh dengan memecahkan lama
waktu menjadi banyak interval waktu yang singkat, kemudian dikalikan dengan
lama waktu tiap interval dengan salah satu kecepatan di interval tersebut, dan
kemudian menambahkan total keseluruhan jarak yang didapat. Konsep dasarnya
adalah, jika interval waktu sangat singkat, maka kecepatan dalam interval
tersebut tidak berubah banyak. Namun, penjumlahan Riemann hanya memberikan
nilai perkiraan. Kita harus mengambil sebuah limit untuk mengdapatkan hasil
yang tepat.
Integral dapat
dianggap sebagai pencarian luas daerah di bawah kurva f(x), antara dua
titik a dan b. Jika f(x) pada diagram di samping
mewakili kecepatan yang berubah-ubah, jarak yang ditempuh antara dua
waktu a dan b adalah luas daerah S yang diarsir.
Untuk
memperkirakan luas, metode intuitif adalah dengan membagi jarak
antar a dan b menjadi beberapa segmen yang sama besar,
panjang setiap segmen disimbolkan Δx. Untuk setiap segmel, kita dapat
memilih satu nilai dari fungsi f(x). Nilai tersebut misalkan
adalah h. Maka luas daerah persegi panjangan dengan lebar Δxdan
tinggi h memberikan nilai jarak yang ditempuh di segmen tersebut.
Dengan menjumlahkan luas setiap segmen tersebut, maka didapatkan perkiraan
jarak tempuh antara a dan b. Nilai Δx yang lebih kecil
akan memberikan perkiraan yang lebih baik, dan mendapatkan nilai yang tepat
ketika kita menngambil limit Δx mendekati nol.
Simbol dari integral adalah , berupa S yang
dipanjangkan (singkatan dari "sum"). Integral tertentu ditulis
sebagai
dan dibaca "Integral
dari a ke b dari f(x) terhadap x."
Integral tak tentu, atau anti derivatif, ditulis:
TEOREMA DASAR KALKULUS
Teorema dasar
kalkulus menyatakan bahwa turunan dan integral adalah dua operasi yang saling
berlawanan. Lebih tepatnya, teorema ini menghubungkan nilai dari anti derivatif
dengan integral tertentu. Karena lebih mudah menghitung sebuah anti derivatif
daripada mengaplikasikan definisi dari integral, teorema dasar kalkulus
memberikan cara yang praktis dalam menghitung integral tertentu.
Teorema dasar kalkulus menyatakan: Jika sebuah
fungsi f adalah kontiniu pada interval [a,b] dan jika F adalah fungsi yang
mana turunannya adalah f pada interval (a,b), maka
Lebih lanjut, untuk setiap x di interval (a,b),
APLIKASI KALKULUS
Kalkulus
digunakan di setiap cabang sains fisik, sains komputer, statistik, teknik,ekonomi, bisnis, kedokteran, kependudukan, dan di
bidang-bidang lainnya. Setiap konsep di mekanika klasik saling berhubungan melalui kalkulus. Massa dari
sebuah benda dengan massa jenis yang tidak
diketahui, momen inersia dari
suatu objek, dan total energi dari sebuah objek dapat ditentukan dengan
menggunakan kalkulus. Dalam subdisiplin listrik dan magnetisme,
kalkulus dapat digunakan untuk mencari total fluks dari sebuah medan elektromagnetik .
Contoh historik
lainnya adalah penggunaan kalkulus di hukum gerak Newton, diekspresikan
dengan laju perubahan yang merujuk pada turunan: Laju
perubahanmomentum dari sebuah benda adalah sama dengan resultan gaya yang
bekerja bada benda tersebut dengan arah yang sama. Bahkan rumus umum dari
hukum ke-dua Newton: Gaya = Massa × Percepatan, mengandung
diferensial kalkulus karena percepatan bisa diekspresikan sebagai turunan dari
kecepatan. Teori elektromagnetik Maxwell dan teori relativitas Einstein juga
diekspresikan dengan diferensial kalkulus.


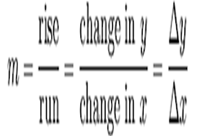


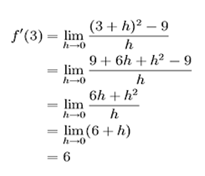






Komentar
Posting Komentar