Langsung ke konten utama

DIMENSI TIGA PRISMA

PRISMA



Definisi Prisma

Prisma yaitu salah satu bentuk bangun ruangyang memiliki beberapa tipe dan dapat dibedakan dari tiap sisinya. Ada prisma segitiga, segi empat, persegi, dan segi lima.
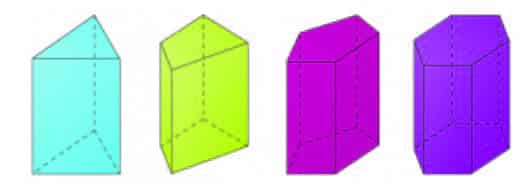
jenis prisma
jenis prisma
Pada bangun ruang ada volume atau isi yang mempunyai ukuran tertentu. Prisma merupakan bangun ruang tiga dimensi yang dibatasi pada dua sisi segi banyak yang sejajar dan juga kongruen.

Pengertian Prisma Segitiga

Prisma Segitiga adalah sebuah bangun ruang tiga dimensi yang terdiri dari alas, penutup dan selimut.
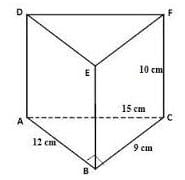
Perhatikan gambar prisma segitiga dibawah ini.
Prisma segitiga diatas memiliki 5 buah sisi, 9 buah rusuk dan 6 buah titik sudut. Limas dengan alas dan tutup disebut Balok dan prisma dengan alas dan tutup berbentuk lingkaran disebut dengan tabung. Prisma memiliki ciri terdapat sisi-sisi yang saling berpotongan menurut rusuk-tusuknya yang sejajar. Berikut ini rumus luas dan volume prisma.

Rumus Luas Prisma

Rumus Volume
Luas alas x Tinggi Prisma
Rumus Luas
(2.luas alas )+ luas selubung
Catatan
Untuk menghitung luas prisma, Hitung terlebih dahulu luas masing-masing sisinya lalu jumlahkan luas sisi-sisi prisma tersebut.

Rumus Volume Prisma

Volume Prisma Segitiga
(1/2 . alas segitiga . tinggi segitiga) . tinggi
Volume Prisma Persegi
(sisi x sisi) . tinggi
Volume Prisma Segiempat
(panjang x lebar) . tinggi
Volume Prisma Segilima
(5 x (1/2 . alas segitiga . tinggi segitiga)) . tinggi

Jaring Jaring Prisma Segitiga

Seperti pada bangun ruang 3 dimensi lainya, prisma jugamemiliki jaring-jaring, Berikut ini adalah gambar jaring-jaring prisma segitiga
jaring jaring prisma segitiga
jaring jaring prisma segitiga

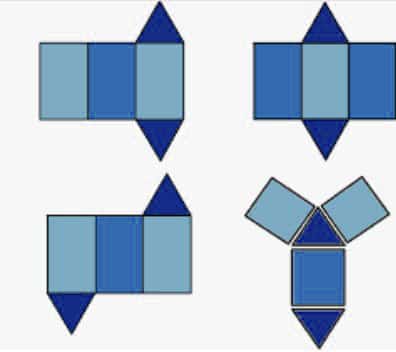
Sifat Prisma Segitiga

Seperti prisam pada umumnya, masing-masing prisma mempunyai ciri untuk membedakan antara prisma satu degan yang lainya, Berikut ini adalah ciri-ciri atau sifat prisma segi tiga
Alas dan atap tetap kongruen.
Sisi sampingnya memiliki bentuk persegi panjang
Mempunyai rusuk yang tegak
Diagonal bidang sisi sama dan berukuran sama

Contoh Soal

Contoh menghitung Luas Permukaan
Soal 1
Tentukanlah luas permukaan prisma jika diketahui :
  • a.s = 15 cm
  • t.s = 18 cm
  • t = 25 cm
Ditanyakan:
Luas permukaan prisma … ?
Jawab
  • Masukkan nilai yang diketahui dalam rumus,
    Luas permukaan Prisma = 18 x {15 + (3 x 25)}
    = 18 x (15 + 75)
    = 18 x 90
    = 1620 cm2
Di dapatkan luas permukaan yaitu : 1620 cm2
Soal 2
Perhatikan gambar dibawah ini dan tentukan Luasnya
tentukanlah luasnya
tentukanlah luasnya
Jawab :
Karna bagian selimut memiliki persegi panjang yang berbeda maka
Luas selimut yaitu luas persegi panjang 1 di tambah dengan luas persegi panjang 2 di tambah luas persegi panjang 3
Luas selimut nya adalah CB x CF + AB x AD + AC x CF
= 9 . 10 + 12 . 10 + 15 . 10
= 90 + 120 + 150
= 360 cm2
Luas alas bawah dan atas yaitu 2 . 1/2 . AB . BC
= 2 x 1/2 x 12 x 9
= 108 cm2
= 108 + 360 = 468 cm2
Contoh menghitung Volume Prisma Segitiga
Jika sebuah tenda kemah memiliki bentuk mirip dengan prisma segitiga dan memiliki tinggi = 150 cm kemudian panjang alas segitiga yang ada pada prisma adalah 200 cm serta tinggi segitiga adalah 130 cm.
Berapakah volume prisma itu ?
Diketahui:
a.s adalah 200 cm
t.s adalah 130 cm
t adalah 150 cm
Volume prisma … ?
Jawab
Pakai rumus volume prisma segitiga
Volume= 1/2 x a.s x t.s x t
Kemudian masukkan nilai yang diketahui dalam rumus,
1/2 x 200 x 130 x 150
1.950.000 cm3
Maka, volume prisma tenda tersebut adlah 1.950.000 cm3

Daftar Pustaka  
http://rumus-matematika.com/rumus-prisma/

Komentar

Posting Komentar

Postingan populer dari blog ini

DIMENSI DUA PERSEGI

PERSEGI PENGERTIAN PERSEGI Persegi  adalah bangun datar  dua dimensi  yang dibentuk oleh empat buah  rusuk    yang sama panjang dan memiliki empat buah  sudut yang kesemuanya adalah  sudut siku-siku . Bangun ini disebut juga sebagai  bujur sangkar . Perhatikan Gambar di bawah ini. Gambar di bawah ini adalah sebuah persegi ABCD. Bagaimana panjang setiap sisi dan besar setiap sudut persegi tersebut?   Jika Anda memperhatikannya dengan seksama, maka Anda akan memperoleh bahwa: sisi-sisi persegi ABCD sama panjang, yaitu AB = BC = CD = AD; sudut-sudut persegi ABCD sama besar, yaitu  sudut  ABC =  sudut  BCD = sudut  CDA =  sudut  DAB = 90°. sifat-sifat persegi sebagai berikut. Semua sifat persegi panjang merupakan sifat persegi. Suatu persegi dapat menempati bingkainya dengan delapan cara. Semua sisi persegi adalah sama panjang. Sudut-sudut suatu persegi dibagi dua sama bes...
1 komentar
Baca selengkapnya

Matematika Zaman Mesir Kuno

Sejarah Matematika Zaman Mesir Kuno Mesir adalah negara yang kaya akan peninggalan sejarah yang sungguh mengagumkan. Tidak hanya piramida yang masih berdiri kokoh namun meraka bangsa mesir dahulunya sudah mengenal matematika dan geometri sebagimana yang kita pelajari sekarang. Asas-asas matematika yang terdapat dimesir itu dimulai pada masa pemerintahan kerajaan beraja,   Firaun yang Masyur pada sekitar 3100 S.M. 1.      Papyrus Bangsa mesir kuno itu pada awalnya juga telah mengenal alat tulis sederhana menyerupai kertas yang disebut papyrus, papyrus ini ada 2 yaitu papyrus rhind dan papyrus moskow. Mereka membuat tulisan berbentuk gambar-gambar dengan menggunakan sejenis pena dengan tinta berwarna hitam atau merah. Papyrus adalah kertas kaku yang dibuat dari buluh papyrus. Orang mesir merekatkan lembaran menjadi gulungan perkamen. Tulisan Mesir Kuno diperkirakan berkembang pada tahun 3400 SM.   Tulisan pada zaman mesir ini ditulis dari kata papu...
Posting Komentar
Baca selengkapnya